本网讯（通讯员 唐瑞雪）12月10日上午，应金沙集团1862cc成色陈波教授邀请，美国加州大学圣迭戈分校吉拉·谢尔（Gila Sher）教授在线上做了题为“逻辑后承”（logical consequence）系列讲座的第二讲。讲座由陈波教授主持，湖南科技大学马克思主义学院颜中军教授担任评议人，来自国内外的300余名听众参加本次线上讲座。

在本次讲座中，谢尔教授围绕“塔斯基所给出的逻辑后承的语义定义是否满足形式性和必然性”问题展开，指出该语义定义面临着形式性、逻辑性、必然性的三重挑战。她从基础整体主义（foundational holism）出发，根据极大不变（maximal-invariance）给出逻辑性的标准：一个性质P是逻辑的当且仅当P是同构不变的。然后通过论证逻辑性等于形式性，形式性蕴涵必然性，进而得出逻辑后承的语义定义满足形式性和必然性的结论。

首先，谢尔教授指出，虽然塔斯基认为自己给出的逻辑后承的语义定义满足形式性和必然性的要求，但事实上他没有给出证明。此外，塔斯基没有明确解释“形式性”“必然性”和“模型”这三个概念，他还提出了关于逻辑性（logicality）的开放性问题，即如何区分逻辑常项与非逻辑常项。如果我们随意地区分逻辑常项与非逻辑常项，这会影响它在模型中的指称（denotation）。而逻辑后承的语义定义为：语句S是语句集Γ的逻辑后承，当且仅当Γ的每个模型都是S的模型。因此，如果我们没有区分逻辑常项与非逻辑常项的明确标准，那么可能会导致逻辑后承的语义定义失效。因此，为了使逻辑后承的语义定义发挥其应有的作用，我们需要找到区分逻辑常项与非逻辑常项的标准。综上，逻辑后承的语义定义面临着形式性、必然性和逻辑性的三重挑战。

谢尔教授指出，逻辑性问题与逻辑后承语义定义的形式性、必然性之间具有紧密的联系。如果我们可以找到一个识别逻辑常项的恰当标准，并且这个标准可以产生形式性和必然性的逻辑后承，那么就可以很好地回应上述三重挑战。因此，我们的首要任务是确立识别逻辑常项的标准。

谢尔教授从不变性（invariance）入手来确立识别逻辑常项的标准。不变是一种二元关系，通常表示为：X在Y下不变（X is invariant under Y），意思为x不受y的改变的影响。例如，将塔斯基替换为弗雷格，“是一位逻辑学家”不变，意思是我们用“弗雷格”替换语句“塔斯基是一位逻辑学家”中的“塔斯基”，不会改变语句的真值。也就是说“是一位逻辑学家”无法将弗雷格与塔斯基区别开。注意，这种不变是将X视为性质，将Y视为关于个体的双射替换函数（replacement-function）。因此，在这里所讨论的“不变”是性质不变（property-invariance）。同时，谢尔教授指出，如果想要更加准确地识别性质的不变性，我们不仅要考虑现实世界中的个体，而且还要考虑反事实个体（counterfactual individuals）。例如，如果将个体域限定为现实世界，那么将一个个体替换为另一个个体，性质“有心脏”与“有肾脏”都是不变的。但是如果考虑反事实个体，那么将一个个体替换为其他个体，这两个性质则不具有不变性。在这里，我们是在常识、直觉的意义上来谈论反事实个体，并没有明确限定它们的范围。在此基础上，谢尔教授给出了“性质p在替换函数r下是不变的”的定义：对于任何性质P和个体域D，P在D中的自变元为β，D上的替换函数r（其中r的取值范围为D₁），β在r下的相为β₁。P在r下是不变的，当且仅当β在D中有性质P当且仅当β₁在D₁也具有性质P。

然后，谢尔教授通过如下四个论题来探究逻辑性、必然性、形式性三者之间的关系。

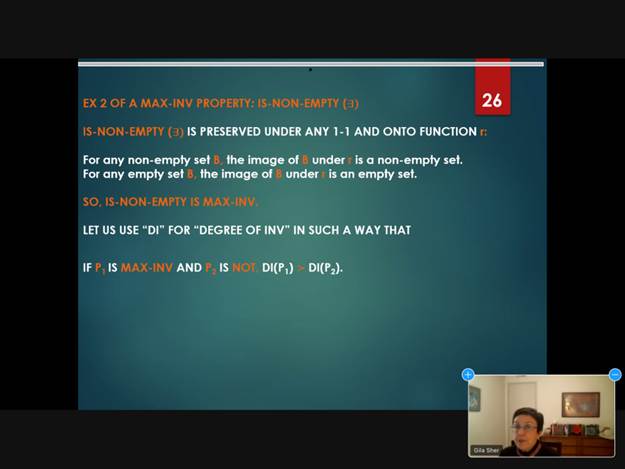
（1）每一个性质在关于个体的双射替换函数下都是不变的。因为当我们将替换函数r确定为同一函数时，每个个体的替换还是它自身，因此在这种情况下，每一个性质都具有不变性。

（2）有些性质具有更高程度的不变性，我们称之为极大不变性（maximal-invariance）。性质P是极大不变的，当且仅当在P所有的替换函数r下都是不变的。P是极大不变，意思是P不对任何个体进行区分，适用于所有个体。如非空性（non-emptiness）、同一性都是极大不变的。在此基础上，谢尔教授给出了逻辑性的判断标准：性质P是逻辑的当且仅当它是极大不变的。一个谓词常项（predicate constant）是逻辑的当且仅当它指称一个逻辑性质。

（3）极大不变是形式性的一个标志。因为P是极大不变的，当且仅当P是同构不变的（isomorphism-invariance），即在所有与P的结构具有同构关系的结构下是不变的。同构不变只在不同的形式模式（formal pattern）之间进行区分，因此同构不变标准也是形式性的标准。因此，逻辑性等同于极大不变性，等同于形式性。

（4）形式性蕴涵必然性。这是因为如果P具有形式性，即P是极大一致的，那么P就不在任何两个个体之间进行区分，因而正确描述P的规律L也不在任何两个个体之间进行区分，因此L是必然的。

综上，从逻辑性等同于形式性，形式性蕴涵必然性，可以推出逻辑性蕴涵必然性。这个结论可以帮助我们去回应逻辑后承语义定义面临的必然性和形式性的挑战。因为逻辑后承是由语句的逻辑性决定的，而语句的逻辑性是由逻辑常项决定的。根据上面的分析，可知逻辑常项具有形式性，即极大不变性，而从极大不变性可以推出形式性，进而推出必然性。因此，逻辑后承具有形式性和必然性。

在讲座最后，谢尔教授指出，虽然她与塔斯基都是根据不变性来确立区分逻辑常项的标准，但两人对不变性的标准有不同的认识。塔斯基认为不变为置换不变（permutation-invariance），而自己认为不变为同构不变。她举例说明，根据置换不变来定义逻辑后承存在反例，因此置换不变不是一个正确的标准。

在评议环节，颜中军教授围绕“令人满意的逻辑常项的标准所要满足的条件”、“形式性的完整涵义”和“形式性与逻辑性的关系”三个主题分别进行提问。首先，他认为，谢尔教授在报告中并没有明确给出识别逻辑常项的标准所要满足的要求。关于这个问题，我们可以从塔斯基关于真的定义中获得一些启发。塔斯基认为，一个令人满意的定义要具备实质上适当（materially adequate）、形式上正确(formally correct)两个条件。但是亨迪卡（Jaakko Hintikka）对塔斯基给出的要求并不满意，提出了真定义所要满足的5个条件。谢尔教授在文章中提到对于形式性和必然性挑战的通常的解决方式要满足的三个条件。但是这些要求并不明确，并且在很大程度上依赖塔斯基关于逻辑后承的语义定义。其次，颜中军教授指出，谢尔教授主张塔斯基没有证明逻辑后承语义定义满足必然性和形式性的要求，但是并没有给出明确且完整的对形式性的定义。最后，他认为谢尔教授关于形式性和逻辑性关系的证明中有循环论证的嫌疑。谢尔教授在强结构的意义上将形式性等同于同构不变（即逻辑性），同时又主张在同构不变的意义上，强结构可以被自然地视为形式性。因此，存在着从逻辑性（形式性）到同构不变到形式性（逻辑性）的循环。

在回应环节，谢尔教授对颜教授第一个问题回应说，自己是从基础整体主义出发来探究逻辑的基础性问题。基础整体主义将我们的知识视为一个由相互联系的不同部分构成的整体。借助“纽拉特之船”的比喻，她主张我们为了获得对世界的认识，需要从已有的知识出发，利用一切可以利用的资源，运用我们的批判性和创造性进行理论化，获得新的知识，同时利用这些新知识去检查已有的知识，修改、替换其中有问题的地方。我们具有关于逻辑常项的一些知识，但并不足以明确对它们进行区分。我们提出关于区分逻辑常项的假设，然后运用该假设去检验人们在日常生活中对逻辑常项的使用，根据这个结果反过来修正我们的假设。关于形式性的问题，她主张，自己是通过同构不变或者极大不变来说明形式性。但是，要完全弄清楚形式性，还有更多的工作要做。关于论证中是否涉及循环的问题，自己从基础整体主义出发来论证，论证的关键在于形式性、同构不变、逻辑性三者的关联性，并不是循环论证。

陈波教授就“非空性似乎不是极大不变的”、“如何看待维特根斯坦对同一的看法”、“报告中的必然性与克里普克所讲的形而上学必然性的区分”进行提问。谢尔教授通过区分一阶性质和二阶性质来回应第一个疑问。维特根斯坦在《逻辑哲学论》中主张，说两个事物是同一的，这是无意义的（nonsense）；而说一个事物与自身同一，这等于什么也没有说。谢尔教授回应说，自己并不完全赞同维特根斯坦的观点。说一句话无意义，是在直觉和普遍的意义上来说的，但是在谈论像逻辑这样的事物时，我们要更准确的谈论。如果认为这句话是精确地说出，那么说一句话无意义，相当于说这句话为假。但这与我们在理论上理解逻辑无关。对于“形而上学必然性”，谢尔教授推测克里普克是从直觉的意义上来谈论的，但是直觉难以琢磨，论证可信度存疑。而自己讲座中所谈到的“必然性”是形式必然性，它是比形而上学必然性次一级的必然性，可以进行更加严格的定义。

（编辑：邓莉萍   审稿：刘慧）