本网讯（通讯员杨新宇、时尚）5月30日和6月6日，纽约市立大学教授、算术模型论领域专家Roman Kossak通过线上平台作了两场“关于算术模型论”的讲座。讲座由金沙集团1862cc成色科学技术哲学教研室程勇教授主持。每场讲座的观众平均超过200余人次。

第一场讲座主题为“Milestones and Small Steps in Model Theory of Arithmetic”。Roman Kossak教授梳理了算术模型论这一领域的研究历史，分为三个发展阶段进行介绍。

第一个阶段是上世纪50-70年代中期，Skolem对Peano算术非标准模型的超幂构造和Ryll-Nardzewski关于Peano算术不能有穷公理化的证明是这一领域的奠基性结果，而Mostowski则在1955年提出了算术模型论研究的纲领性的几个问题。随后Tennenbaum、Scott和Friedman等人从可计算性的角度研究了Peano算术的非标准模型，特别是引入了Scott集的重要概念。Ehrenfeucht和Robinson则从可定义性的角度入手，引入了非标准语言的概念，进而得到了Tarski真不可定义定理的模型论证明。另一个重要的问题是模型的扩张，Kossak教授介绍了尾节扩张（end extension），共尾扩张(cofinal extension)和极小扩张(minimal extension)等概念和MacDowell-Specker定理、Gaifman分裂定理等重要结果。

第二阶段是对同构不变量(isomorphism invariants)的研究，Kossak教授重点介绍了两个著名的未解问题: Harvey Friedman第14问题和Scott集问题。对Peano算术的一个完备扩张T，T的模型的序归约构成了一个类Ord(T)，那么Ord(T)是否依赖于T呢？这是Harvey Friedman第14问题。而Scott集问题的内容则是，每一个Scott集是否是某个Peano算术的非标准模型的标准系统（standard system）？我们已知这一问题在连续统假设下答案是肯定的，但若不考虑连续统假设，这一问题的答案仍是未知的。

第三阶段是对递归饱和模型的研究，由于时间关系Kossak教授没有对这一部分作过多介绍，而第二场讲座正是关于这一主题的。

在评论环节，金沙集团1862cc成色时尚同学就不完全性定理的模型论证明进路向Kossak教授提问，Kossak教授简要梳理了Indicator方法的发明及其在证明独立性语句方面的强大作用；程勇教授则提出了三个问题：力迫法和算术模型论的联系；在具体不完全性研究中证明论和模型论方法的比较；当前算术模型论研究的前沿问题。对于第一个问题，Kossak教授回顾了Simpson在1974年发表的“Forcing and Models of Arithmetic” 一文；对于第二个问题，Kossak教授指出二者相互补充，证明论方法在某些方面更加有效，但模型论方法可以描绘一个宏观的图景；对于第三个问题，Kossak教授介绍了模型的子结构格这一领域的一些进展和尚未解决的难题。

第二场讲座主题为“Undefinability and Absolute Undefinability in Arithmetic”。Kossak教授深入地介绍了“可定义集(definable sets)”和“绝对不可定义集(absolutely undefinable sets)”。一个集合是可定义的，即可以找到一个公式（称为定义公式），使得一个元素属于该集合当且仅当满足定义公式。然后Kossak教授介绍了在一些常见的算术结构中，哪些集合是可定义的，哪些集合是被证明不可定义的。比如序关系在(N,S)，即含有后继关系的自然数结构中是不可定义的、加法在(N,*,S)中是可定义的、真理集在(N,+*)中是不可定义的，但如果限制到固定的公式层级上是可定义的。但是值得注意的是，如果我们把逻辑系统拓展到表达力更强的无穷逻辑          ，则可以在公式中使用无穷次析取或合取，那么许多在一阶逻辑下不可定义的集合就会变成可定义的。

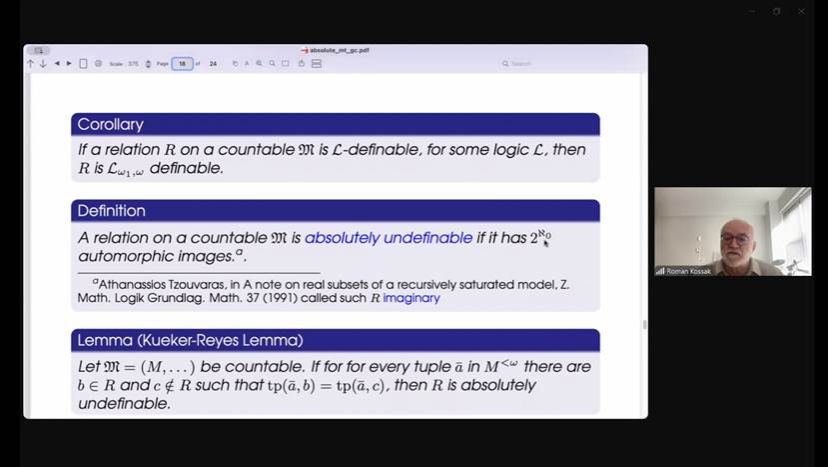
之后Kossak教授介绍了“荣美集(resplendence)”的概念。Barwise等人证明了一个可数集合是递归饱和的当且仅当它是荣美的。Kossak教授还给出了荣美集更多的性质，以及在分体论的应用。Kueker证明了在一个可数结构中，一个集合R是            可定义的当且仅当R有至多自然数基数个自同构像，当且仅当少于连续统个自同构像。这里Kossak教授自然地引入了绝对不可定义的定义：一个集合是可定义的当且仅当它有连续统个自同构像。由Kueker-Reyes定理，我们可以推出，任意不是绝对不可以定义的集合           中都是参数可定义的。之后Kossak教授介绍了在一些具体的常见模型中的绝对不可定义和递归饱和。

在评论环节，程勇教授提问绝对不可定义的概念提出初衷是什么。Kossak教授回答自同构像一直是模型论中研究的一个重要问题，绝对不可定义概念的提出是为了解决在一个模型中添加新关系时应该具有哪些性质。之后他们一起讨论 了Kueler定理的细节。

Kossak教授的两场讲座高屋建瓴，深入浅出，既从宏观上给出了算术模型论这一数理逻辑重要分支的整体图景，又就不可定义性和绝对不可定义性等深刻概念作了细致的探讨。对于刚入门这一领域的年轻学生而言，不失为提供了一张立体直观的鸟瞰图；对于从事相关领域研究的成熟学者而言，也有助于其更深入地把握算术的非标准模型这一丰富深邃的研究对象。

（编辑：邓莉萍 审稿：刘慧）